Research

Our overarching goal is to develop theory, algorithms, models, and software for large-scale optimization problems with applications in sustainable energy systems. The fundamentals of our research are mathematical programming, statistics, and machine learning.

Here are several research areas that we currently work on:

Explain Optimization and Machine Learning Models using LLM Nowadays, both optimization models and machine learning models are widely used in various industries. However, these models remain less accessible to practitioners, stakeholders, and operators without a solid technical background. The primary barrier is that non-experts often encounter difficulty conveying their ideas to models or interpreting model responses. This disconnection between natural language and domain-specific language leads to ineffective collaboration between non-technical and technical teams and a lack of conviction regarding model outcomes. A first-of-its-kind system that enables natural language-based diagnosis and troubleshooting for infeasible optimization models using LLM is proposed in our recent work. Our ongoing efforts are directed towards extending the functionalities and applicability of our system, to make mathematical optimization and machine learning models more explainable and accessible.

Sustainable energy systems design The major economies in the world including the U.S., EU, and China all have set their goals to achieve net-zero carbon emission in the next few decades. As process systems engineers, we aim to design sustainable energy systems to help transition to the carbon-neutral future. The new designs incorporate the chemical industry, the power systems that have both thermal and renewable generation sources, the natural gas system, etc. The tightly coupled energy systems could yield significant economic and environmental benefits. In addressing this problem, large-scale optimization problems have to be solved because of the spatial and temporal complexity of the problems that integrate design and operating decisions and under high uncertainty. In addition, the huge amount of data from different industries have to be processed in meaningful ways. To develop capabilities for solving these problems, we have to advance the field of mathematical optimization and machine learning.

Data-driven optimization under uncertainty Uncertainties are prevalent in real-world decision-making processes due to changing conditions, long-term forecasts, inaccurate measurements, or lack of information. For example, uncertainties in supply chain management can arise from future customer demands, potential network disruptions, or even the spread of a pandemic. Failing to consider uncertainties in the decision-making process may lead to suboptimal or even infeasible solutions. Despite the prevalence of uncertainties involved in process systems, very few uncertainty-aware decision support tools have been used in practice. To address this challenge, we have been developing algorithms and software for a mathematical framework called stochastic programming, which optimizes the expected objective, such as expected cost, over all the possible realizations of the uncertainties. We are especially interested in problems under the uncertainty of rare events, such as extreme weather including wildfire, hurricanes, and snowstorms, that cause supply chain disruption or power systems blackout. The aim is to design reliable and economic supply chain and energy infrastructure using these mathematical frameworks.

Machine learning for discrete and global optimization Decision-making in process systems engineering typically involves discrete variables and nonlinear constraints, which give rise to mixed-integer nonlinear programming (MINLP) problems. MINLP problems are NP-hard in general, which means that they suffer from the “curse of dimensionality”. Machine learning or surrogate models are fast to implement but have no guarantee of optimality. However, there are potential benefits in developing machine learning models to accelerate the solution of MINLP problems, where we use techniques including deep learning and reinforcement learning. A recent review of this area can be found here.

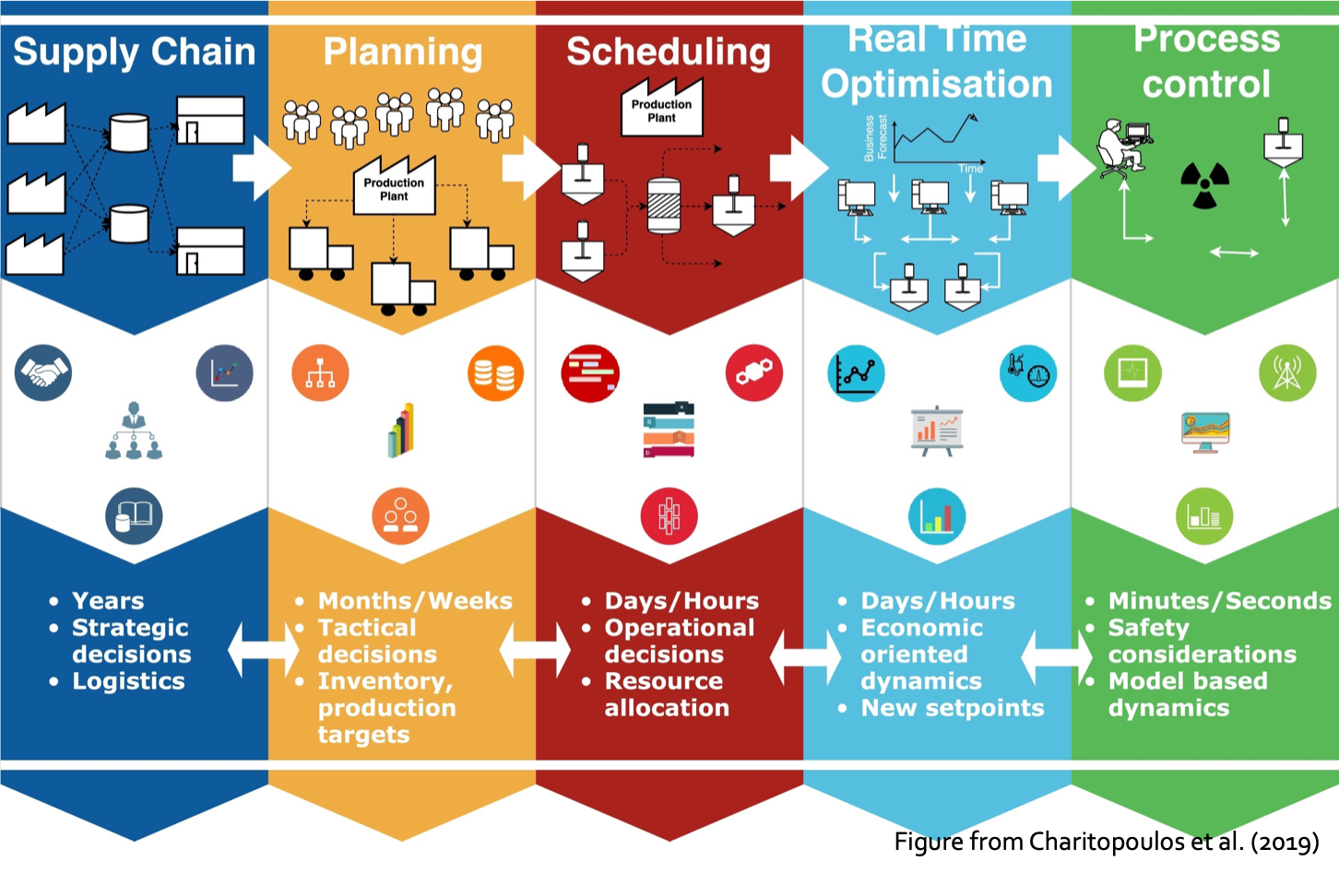
Multi-scale models and algorithms Decision-making in process systems engineering involves large temporal and spatial scales. Strategic decisions are made on a yearly basis, e.g., the supply chain design of a large geographical region. Tactical decisions, such as production targets, are made on a monthly or weekly basis. Scheduling and real-time optimization decisions are made on a daily or hourly basis. Process control of a reactor or flowsheet is made every few minutes or seconds. One could spend his/her career in one of the five levels of the decision-making processes. However, making decisions at the strategic level while neglecting the decisions at lower levels can lead to suboptimal or even infeasible supply chain designs. On the other hand, integrating models at various scales prevents information loss and ensures that models are consistent across scales. It also allows uncertainty to be propagated across scales to ensure that both the true uncertainty and the source of that uncertainty are known. We aim to develop a hybrid multi-scale modeling approach that combines data-driven reduced-order models with rigorous optimization algorithms.

Parallel computing and advanced computational architecture The current revolution in AI and machine learning is largely driven by advances in hardware. We aim to leverage state-of-the-art hardware solving large-scale optimization problems. We plan to develop parallel and distributed algorithms that are amenable to be solved using cloud computing. Graphical Processing Units (GPU) and Tensor Processing Units (TPU) will be used for laborious machine learning tasks. Quantum computing architecture, such as D-Wave quantum annealer will be used for combinatorial optimization problems.